| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- 백준
- Python
- 동적 계획법
- BFS
- Javascript
- DFS
- frontend
- DP
- git
- VIM
- 알고리즘
- 자바
- react
- Database
- db
- 그레이들
- Data Structure
- 프로그래머스
- LeetCode
- 다이나믹 프로그래밍
- CS
- Redux
- Graph
- Algorithm
- TypeScript
- network
- 리트코드
- vscode
- 안드로이드
- java
- Today
- Total
늘 겸손하게
백준 11444 ( C++) 본문
피보나치 수 6
n 번째 피보나치 수를 구하면 되는 문제
이지만 n이 1,000,000,000,000,000,000 보다 작거나 같은 자연수이다.
재귀 함수를 이용하거나 단순하게 반복문으로 F2부터 Fn까지 구하려면 시간 초과가 발생한다.
시간 내에 문제를 해결하려면 다른 방식으로 접근해야 한다.
1. 방정식을 행렬식으로 표현
Fn+2 = Fn+1 + Fn 인 피보나치 수의 공식을 행렬 꼴로 바꾸어야 한다.
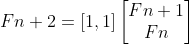
위 식만으로는 부족하므로 식 하나를 더 구한다.
Fn+1을
Fn+1 = Fn+1 + 0 * Fn로 표현 가능하므로

위 두 식을 조합하면
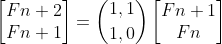
위 식을 얻을 수 있다.
좌변의
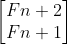
를 u(n+1)로 보면
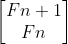
를 u(n)으로 표현할 수 있고
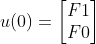
이고
A를
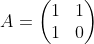
라고 하면
u(n+1) = A * u(n) 이 성립함을 알 수 있다.
이를 통해
u1 = A * u0
u2 = A * u1 = A * ( A * u0 ) = A^2 * u0
u3 = A * u2 = A * ( A * u1 ) = A * ( A * ( A * u0 ) ) = A^3 * u0
u4 = A * u3 = A * ( A * u2 ) = A * ( A * ( A * ( A * u0)) ) = A^4 * u0
.
.
.
u(n) = A^n * u0 임을 알 수 있다.
그러므로
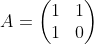
일 때
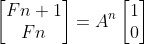
가 성립함을 알 수 있다.
결국 Fn을 알기 위해서는 A^n 행렬의 2행 1열의 원소 값을 알아내면 된다.
2. A^n 구하기
A^n을 구하기 위해 A를 n번 제곱하면 간단하지만 정말 오래 걸린다.
더 빠르게 A^n을 구하기 위해 빠른 거듭제곱 알고리즘을 적용하여 O(N) 시간 복잡도를 O(logN) 시간 복잡도로 단축한다.
빠른 거듭제곱 알고리즘
- N 이 홀수이면 A^N을 A*A^(N-1)로 바꾸고 A를 결괏값에 곱한다.
- N 이 짝수이면 A^N을 (A^2)^(N/2) 즉 A를 제곱하고 N을 2로 나눈다
- N = 0 될 때까지 반복
이를 코드로 표현하면
matrix power(matrix a, ll n) {
ll size = 2; // 길이
matrix res(size, vector<ll>(size)); // 반환할 행렬
for (int i = 0; i < 2 ; i++ ) // 단위 행렬 생성
res[i][i] = 1;
while ( n > 0 ) {
if ( n % 2 == 1 ) {
res = res * a;
}
n /= 2;
a = a * a;
}
return res;
}로 표현 가능하다.
코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
|
#include <iostream>
#include <vector>
using namespace std;
typedef long long ll;
typedef vector<vector<ll>> matrix;
matrix operator * (const matrix & a, const matrix & b) {
ll size = 2;
matrix res(size, vector<ll>(size));
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 2; j++ ) {
for (int k = 0; k < 2 ; k++ ) {
res[i][j] += a[i][k] * b[k][j];
}
if ( res[i][j] >= 1000000007 ) res[i][j] %= 1000000007;
}
}
return res;
}
matrix power(matrix a, ll n) {
ll size = 2; // 길이
matrix res(size, vector<ll>(size)); // 반환할 행렬
for (int i = 0; i < 2 ; i++ ) // 단위 행렬 생성
res[i][i] = 1;
while ( n > 0 ) {
if ( n % 2 == 1 ) {
res = res * a;
}
n /= 2;
a = a * a;
}
return res;
}
int main(void) {
ll n;
cin >> n;
matrix ans(2, vector<ll>(2));
ans[0][0] = 1;
ans[0][1] = 1;
ans[1][0] = 1;
ans[1][1] = 0;
ans = power(ans, n);
cout << ans[1][0];
}
|
cs |

'코딩 문제 > 백준' 카테고리의 다른 글
| 백준 10816 ( C++ ) (0) | 2021.07.19 |
|---|---|
| 백준 1920 ( Java ) (0) | 2021.07.18 |
| 백준 2740 ( C++ ) (0) | 2021.07.16 |
| 문제 1780 (C++) - 종이의 개수 (0) | 2021.07.14 |
| 백준 1676 ( Java ) - 팩토리얼 0의 개수 (0) | 2021.07.11 |



