| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- TypeScript
- react
- network
- frontend
- db
- 프로그래머스
- VIM
- Javascript
- 그레이들
- 백준
- Python
- Data Structure
- DFS
- 자바
- LeetCode
- Redux
- 알고리즘
- Algorithm
- Database
- DP
- 안드로이드
- vscode
- CS
- java
- 동적 계획법
- 다이나믹 프로그래밍
- git
- 리트코드
- BFS
- Graph
- Today
- Total
늘 겸손하게
정렬 알고리즘 정리 - Python 본문
1.Bubble sort
버블 정렬
서로 인접한 두 원소를 비교하고 왼쪽 원소가 오른쪽 원소보다 크기가 클 경우 서로 값을 교환하여 정렬하는 방식
원소의 이동이 거품이 수면으로 올라오는 모습으로 보여서 버블 정렬로 불리게됨
구현은 간단하나 효율성은 많이 떨어지는 정렬 알고리즘
알고리즘
1. 첫 번째 원소와 두 번째 원소, 두 번째 원소와 세 번째 원소, 세 번째 원소와 네 번째 원소, ...., 마지막-1 원소와 마지막 원소를 비교하여 n -1번째 원소가 n번째 원소보다 큰 경우 교환
2. 1번 과정이 끝나면 가장 큰 원소가 배열 맨 뒤로 이동하므로 배열 마지막 원소를 제외한 나머지 원소들을 가지고 1번 과정을 다시 수행
3. 배열이 완전히 정렬될때까지 1,2번 과정 반복
시간복잡도
최선, 평균, 최악 모두 O(N ^ 2)
def bubble_sort(arr):
N = len(arr)
for i in range(N):
for j in range(1, N - i):
if arr[j-1] > arr[j]:
arr[j-1], arr[j] = arr[j], arr[j-1]
2. Selection Sort
선택 정렬
원소를 저장할 위치(인덱스)는 정해져 있고, 어떤 원소를 넣을지 선택하는 알고리즘
알고리즘
1. 배열에서 최소값을 찾는다.
2. 최소값, 배열의 첫 번째 원소값 교환
3. 첫 번째 원소를 제외한 나머지 원소로 1,2번 과정 반복
시간복잡도
최선, 평균, 최악 모두 O(N ^ 2)
def selection_sort(arr):
N = len(arr)
for i in range(N - 1):
indexMin = i
for j in range(i + 1, N):
if arr[j] < arr[indexMin]:
indexMin = j
if indexMin != i:
arr[indexMin], arr[i] = arr[i], arr[indexMin]
3. Insertion Sort
삽입 정렬
2번째 원소부터 시작하여 왼쪽의 원소들과 비교하여 삽입할 위치를 정한 후, 원래있던 원소들을 뒤로(오른쪽) 옮긴 후 빈 자리에 원소를 삽입하여 정렬하는 알고리즘입니다.
알고리즘
1. 두 번째 인덱스부터 탐색 시작. tmp에 해당 인덱스 저장, prev에 해당 인덱스 - 1 저장
2. prev에 저장된 인덱스값이 음수가 되지 않고, tmp 인덱스가 가리키는 원소값보다 prev가 가리키는 값이 크다면 prev가 가리키는 값을 prev + 1에 저장합니다.
3. 2번 과정이 끝나면 prev가 가리키는 값은 tmp가 가리키는 값보다 작은 값들 중 제일 큰 값입니다. 따라서 prev + 1에 tmp가 가리키는 값을 저장합니다.
4. 배열이 정렬될때까지 2,3번 반복
시간복잡도
최악 : O(n ^ 2)
평균 : O(n ^ 2)
최선 : O(n)
def insertion_sort(arr):
for index in range(1, N):
tmp = arr[index]
prev = index - 1
while prev >= 0 and arr[prev] > tmp:
arr[prev + 1] = arr[prev]
prev -= 1
arr[prev + 1] = tmp
4. Quick sort
퀵 정렬
가장 빠른 정렬 알고리즘 중 하나
알고리즘
1. 배열 첫 번째 원소를 가리키는 커서 1개, 마지막 원소를 가리키는 커서 1개, 중앙값 피벗(pivot)을 준비
2. 피벗값보다 크거나 같은 요소를 찾을 때까지 왼쪽 커서를 오른쪽으로 옮긴다.
3. 피벗값보다 작거나 같은 요소를 찾을 때까지 오른쪽 커서를 왼쪽으로 옮긴다.
4. 각 커서가 가리키는 값을 서로 교환
5. 각 커서가 서로 교차할 때까지 반복
6.1~5번 과정을 완료하면 피벗값 이하의 원소들을 가진 배열, 피벗값 이상의 원소들을 가진 배열 두 그룹으로 배열이 나누어진다.
7.1~5번 과정을 두 그룹에 각각 적용한다.
8. 배열이 정렬될때까지 1~7번 과정 반복
시간복잡도
최악 : O(n ^ 2)
평균 : O(logn * n)
최선 : O(logn * n)
정렬속도가 빨라 많이 쓰이는 알고리즘
피벗 선택에 따라서 시간복잡도가 O(n ^ 2)이 되는 최악의 경우가 존재함
def quick_sort(arr, left, right):
lp = left
rp = right
x = arr[(lp + rp) // 2]
while lp <= rp:
while arr[lp] < x: lp += 1
while arr[rp] > x: rp -= 1
if lp <= rp:
swap(arr, lp, rp)
lp += 1
rp -= 1
if left < rp: quick_sort(arr, left, rp)
if lp < right: quick_sort(arr, lp, right)
5. Merge Sort
병합 정렬
분할 정복법을 이용한 정렬 방법
알고리즘
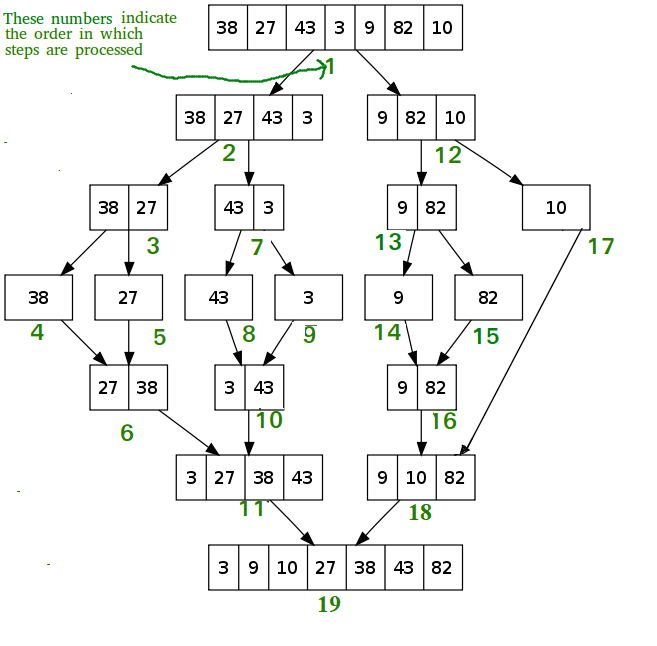
1. 중앙값을 구하고 중앙값을 기준으로 왼쪽 배열, 오른쪽 배열 생성
2. 배열의 길이가 1이 될때까지 배열을 두 개로 쪼개기
3. 쪼개진 배열을 정렬시키며 병합
4. 정렬 -> 병합 과정을 배열이 정렬될때까지 반복
시간복잡도
최악 : O(logn * n)
평균 : O(logn * n)
최선 : O(logn * n)
def merge_sort(arr):
if len(arr) > 1:
mid = len(arr) // 2
L = arr[:mid]
R = arr[mid:]
merge_sort(L)
merge_sort(R)
i = j = k = 0
while i < len(L) and j < len(R):
if L[i] < R[j]:
arr[k] = L[i]
i += 1
else:
arr[k] = R[j]
j += 1
k += 1
while i < len(L):
arr[k] = L[i]
i += 1
k += 1
while j < len(R):
arr[k] = R[j]
j += 1
k += 1
'Algorithm' 카테고리의 다른 글
| 수학식 후위 표기식으로 변경 (차량기지 알고리즘) (0) | 2023.04.10 |
|---|---|
| LIS - 최장 증가 부분 수열 (2) | 2022.09.20 |
| JavaScript - 소수 판별 (0) | 2022.07.15 |
| JavaScript - 순열, 조합 (0) | 2022.07.15 |
| 기초 알고리즘 요약 (0) | 2022.05.13 |
